Smoothing for the CGAL during Google summer of Code 2017

This is a final report on my work for the CGAL project during the 2017 Google summer of code.

My main task was to enhance the Polygon mesh processing package with two algorithms for optimization of a triangulated 3D surface mesh. The first algorithm aims at improving the mesh quality by using geometric criteria such as angles adjacent to mesh vertices and element areas, as proposed in this paper by Surazhsky and Gotsman. The second algorithm is based on the mean curvature flow to calculate and apply an operator to mesh vertices, as proposed by Desbrun et al, which achieves smoothing of the overall shape without necessarily improving the quality of the mesh elements and without being dependent on the discretization.

Code

All commits can be found in this branch in the CGAL repository.

A summary of the project and a list of all commits can be found in this github issue.

Highlights

The underlying challenge: Degenerates

Degenerate edges and faces were the most challenging part. Dealing with them correctly determines not only the robustness of the algorithm but even more so affects severely the final result.

For example, when trying to move vertex xi around xj when trying to equalize angles between vectors e1 and hi, and e2 and hi

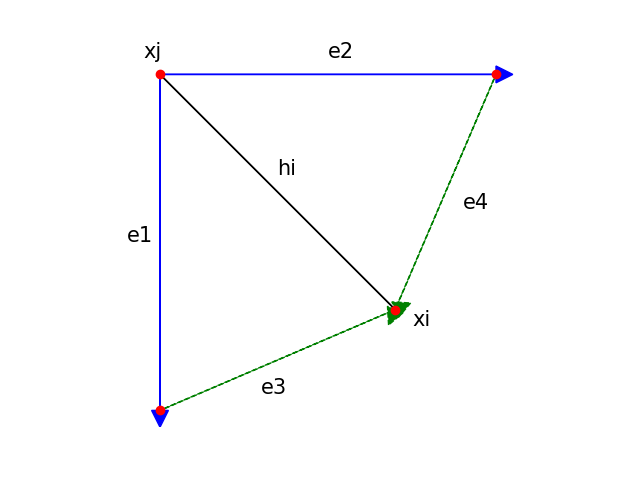
vectors

these degenerate cases may occur:

deg_1 deg_2 deg_3

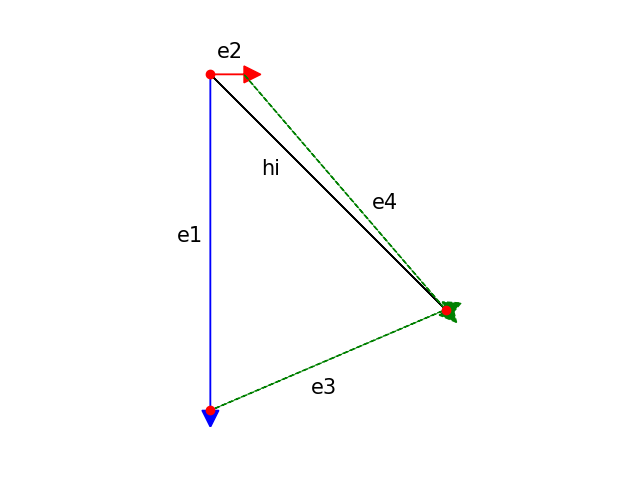
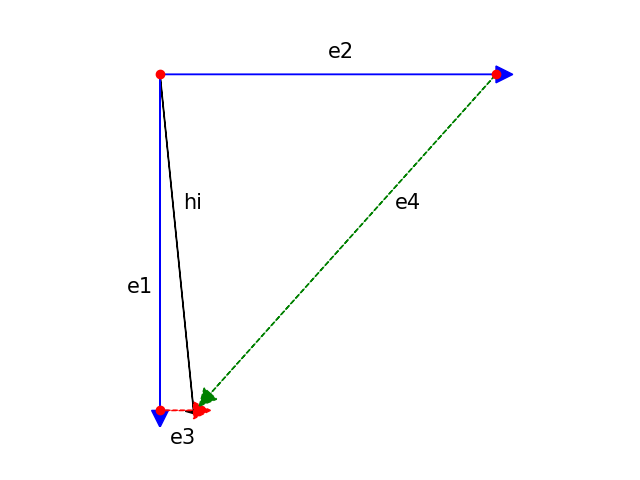
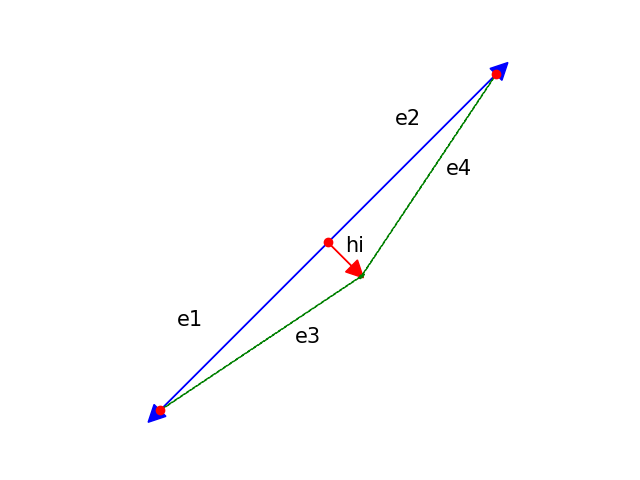
In the first two cases the degenerate edge is treated as having no weight, and does not affect the smoothing process. In the third case however, I decided that it is important to “untangle” as much as possible the vertices, so I used two cross products to find the correct direction on the tangent plane and move the vertex on that. Thankfully the CGAL directories are full of mesh examples with all sorts of degenerate cases to experiment multiple crashes before finding a solution!

During my adventures with degenerate edges and faces I tried to visualize them and actually look at the hidden problem face to (degenerate) face. So I wrote a small feature to shrink a triangulated mesh, with a scale factor given as a parameter. After that, all my fears for degenerates went away.

This looks like a simple triangle formed by 3 smaller triangles,

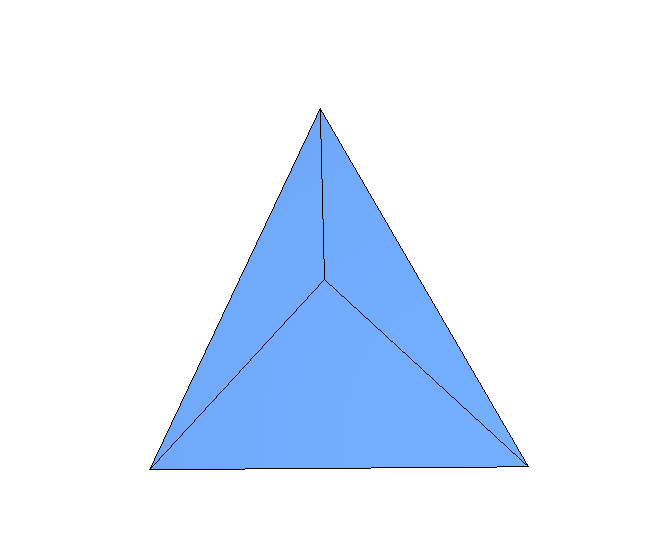
triangle

but in fact it’s formed by 6:

deg_triangle

In other cases more imagination is needed:

deg_face

Projection to original surface

When using angle equalization to calculate a new barycenter for the voronoi area around a vertex, a new location is calculated from the point on which the bisectors meet. However, this location is not the final location of the smoothing process. Depending on the curvature of the area, the new point will most probably be somewhere off the original surface. To tackle this, first calculation of a new location on the tangential plane is performed using the normal direction, and then that point is projected to the original surface using the magnificent Axis Aligned Bounding Box tree that is implemented in CGAL.

Local minima on gradient descent

Area equalization is achieved by minimizing the areas of the triangles around each vertex. In particular, gradient descent is used to find the coordinates that minimize the difference of the areas of all triangles around each vertex to their average.

x_(n+1) = x_n - eta dr/dx

An amazing problem that appeared was that energy was being stuck in local minima. To confront this, I added learning rate annealing based on an approach proposed by L. Bottou.

eta = eta0 / (1 + t0*t)

Bottou proposes an heuristic for the calculation of t0 based on the min eigenvalue of the Hessian matrix of the function that is being minimized, but suggests experimenting with a small dataset and estimating the value of the parameter by trial and error. With such experimenting I found a robust estimation for t0, (with t being the epoch and eta0 an initial guess for the learning rate).

Curvature flow

On the flip side, the mean curvature flow doesn’t care about any equalization or improvement of mesh quality. It is based on the fact that different points have different curvature, and those more curved should be moved more towards the inside so that the result approximates a sphere. No projection or tangential relaxation makes sense.

The curvature - via some sophisticated maths in the paper - translates to cotangent weights of the angles incident to the vertices. Special attention must be paid to - what else - degenerate cases. Here the problem arises here when dealing with 0 or Pi angles, since cot = cos/sin and the sine is 0 for very small or flat angles.

As a first step, all degenerate faces (faces with NULL area) are removed before applying the operator, and even more so, after each movement a degeneracy check takes place. If a face has fallen, so long!

GUI plugin

The CGAL Polyhedron demo is a brilliant GUI that enables quick testing and visualization. Most importantly, since it’s a Qt based application it’s easy to enhance and improve it. It is currently under heavy development. And this is my contribution to it:

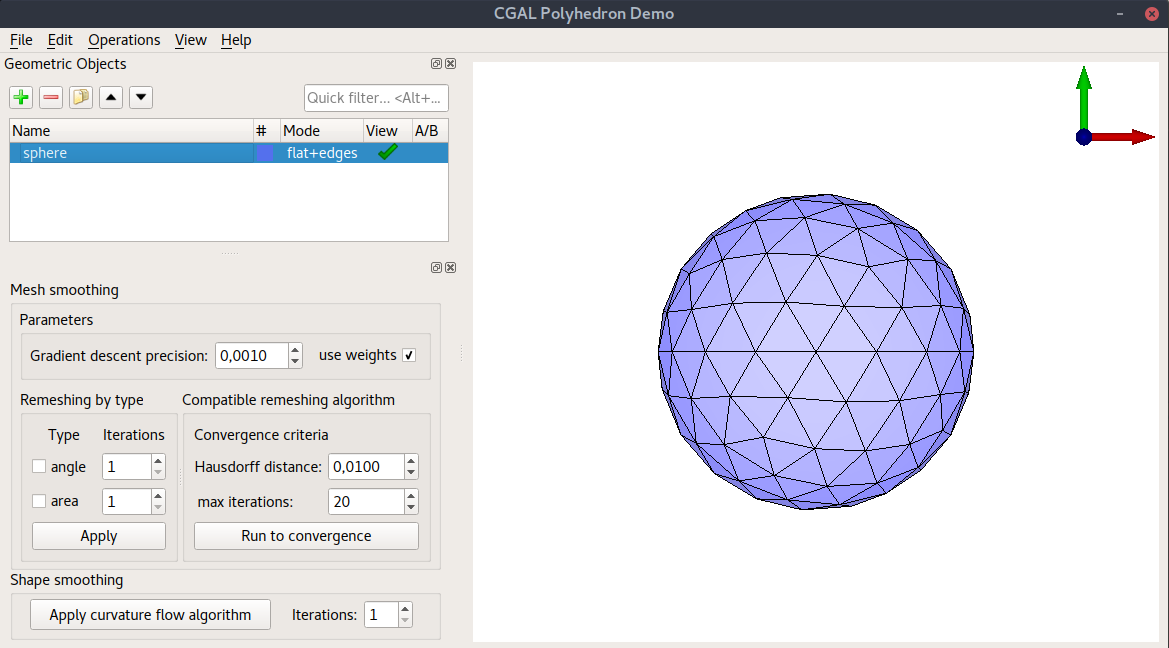
Evaluate the result

How smooth is a mesh? When it comes to mesh smoothing, several approaches may be considered. Calculation of the distribution of the triangle skewness, before and after the smoothing is a bold idea. Others include calculating the Hausdorff distance, or maybe just looking at the minimum value of the angles or areas. Here is an elephant being smoothed and histograms of the aspect ratios or the triangles before and after smoothing:

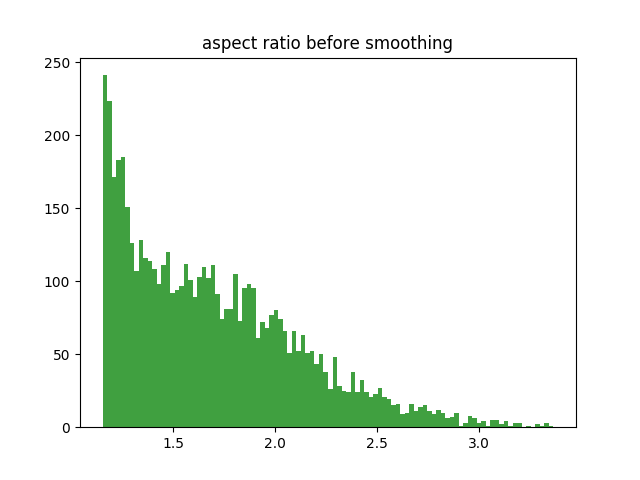
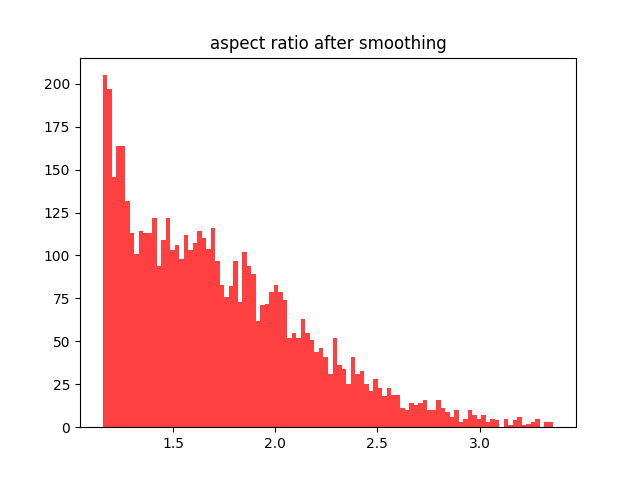
elephant before_smoothing smoothed after_smoothing

The aspect ratio is defined as the ratio of the maximum altitude of a triangle to its minimum edge.

In terms of shape smoothing, it is more difficult to quantify the result. Sharp edges and corners should be smoothed with the overall volume being kept almost equal. As a test flat surfaces do not change at all after applying the operator, since the curvature is zero everywhere. Even more so, a sphere with differently sampled half should remain unchanged, since the curvature is the same everywhere.

Here is shape smoothing with the mean curvature flow applied to the devil gradually:

deg_face deg_face deg_face

Todo