This is how I applied a reinforcement learning algorithm on the snake game. The snake learns to grow with DQN using convolutional layers of states. Code: ai-snake

I managed to trained it to the point where it eats around 12 fruits so far. Not really great, I know.
Reinforcement learning
The algorithm involves estimating a value function given a particular state. The state is a 10x10 array of cell types, including the snake body and head, walls and food. The function that is being calculated for every state (Q-function) is a measure of “how good” each possible action is. The training process is a constant interaction between the agent and the environment. The snake acts on the environment and learns from the outcome of each action. At any step, the snake(agent) may choose to move forward, turn left or turn right. After each step, the environment gives the agent a reward depending on the new state: Zero reward if it stepped on an empty cell, negative reward if it got killed, and if it ate a fruit the reward is positive and equal to its size. The longer the snake, the richer the reward.
The goal of the reinforcement learning algorithm is to find the optimal action-value function. The action-value function indicates the value of taking an action at each case, so optimizing it means finding the best action for any given state. This is achieved by trying to maximize the reward that receives. To obtain a lot of reward, the agent must choose actions that have granted a lot of reward in the past. But to discover such actions, it has to try actions that has never tried before. As such, there is trade-off between exploration and exploitation.
DQN (Deep Q-Network)
The basic algorithm, known as Q-learning, approximates the optimal action-value function over all successive states:
Q(St, αt) ← Q(St, αt) + α [rt + γ · max Q(St + 1, αt) - Q(St, αt)]
α is a constant step size, γ is a discount rate. The discount rate determines the present value of future rewards.
The function is updated with a better estimate using the error (difference) between the current and the next state. This error is the target Rt+1 + γ · Q(St+1) by which a batch of the experience is updated on every step. It is derived from the Bellman equation, which expresses a relationship between the value of a state and the values of successor states.
An artificial neural network (ANN) model is used to approximate the Q-function. The ANN is essentially a vector of weights that get continuously informed. I used TensorFlow’s conv2d convolution layers via the keras API and I used 5 channels of subsequent states as input to the convolution layers of the neural network. In a higher level, the ANN is a model that gives an estimate of the Q-function for a 5-channel state input.
Training
As the algorithm indicates, training is done using an alternative policy. This policy is the experience of the agent and is stored in memory for each step. To train the network weights, a batch is chosen randomly from the accumulated experience. The alternative policy (accumulated experience) is improved in parallel with the agent’s model. The original paper is here.
The following results have been produced with a batch size of 32 and total memory size 6000 over 30000 episodes.
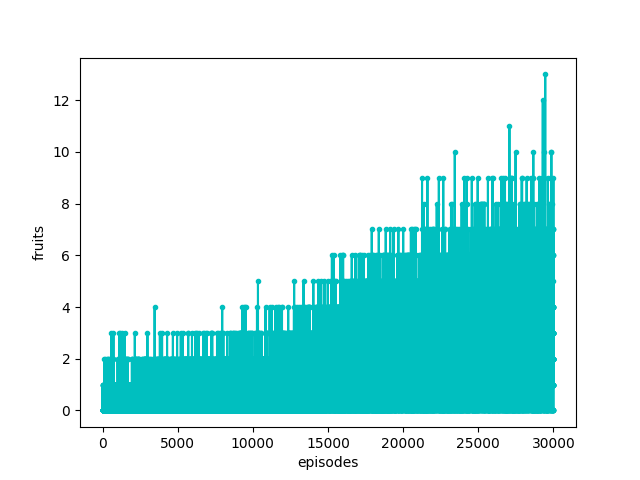
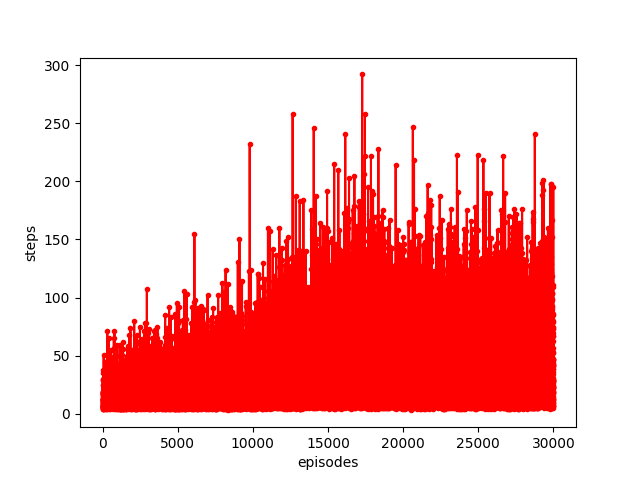
Finally, keeping count of the loss that is returned from tensorflow’s train_on_batch method, which I use, the result does not seem ideal.
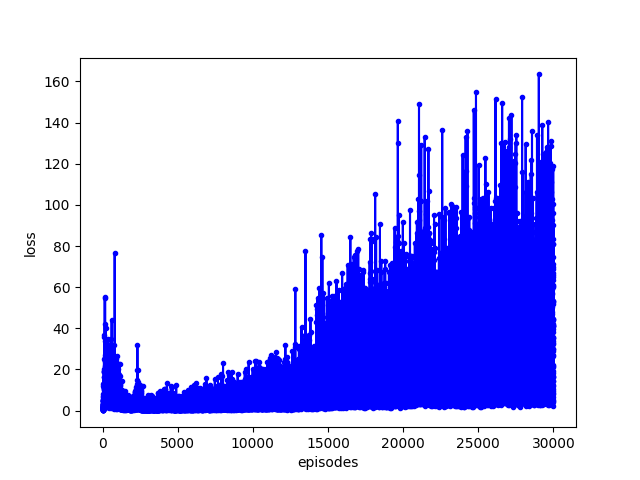
The loss in the figure is summed over all steps on each episode. However, I am not absolutely sure this loss should definately decrease. I am not sure what to make of this, maybe there is a lot of room for improvement! If you know better, please tell me.